October/November 2012
1. Let `w` be the number of white keys and `b` be the number of black keys. Then `w+b = 88` and:
`(w+2)/(w+2+b) = 0.60 => (w+2)/90 = 0.60 => w+2 = 54 => w = 52 => b = 36`
Answer: B
2. Volume of first box is 3×6×5 = 32×2×5. Volume of second box is `k^2 times m` where `k` and `m` are integers with `k >1`, so the only possibility is `k=3` and `m =10`.
Answer: C
3. Let `x` be the first map distance and `y` be the second map distance (in inches), so `x + y =52`. The actual distances are `4/3 x` for Map 1 and `8/7y` for Map 2 (in miles) and we must have
`4/3 x = 8/7 y => y = 28/24 x = 7/6 x => x + 7/6 x = 52 => 13/6 x = 52 => x = 24 => 4/3 x = 32`
Answer: C
4. Let `x`, `y`and `z` be the ages of Anh, Ana and Ann, respectively. Then:
`(x+y+z)/3 = A => x+y+z = 3A`
Amy's age must also be `z`, so:
`(y+z+z)/3 = B => y + 2z = 3B`
We also know that `z = x+12` so `2x+y+12 = 3A` and `y+2(x+12) = 3B => 2x+y+24 = 3B`. Thus:
`3B-3A = 12 => B-A = 4`
Answer: A
5. `(25 text(miles))/(1 text(gallon)) => (1 text(gallon))/(25 text(miles)) times (3.785 text(liters))/(1 text(gallon)) times (1 text(mile))/(1.609 text(km)) approx 0.094 (text(liters))/(text(km)) => 9.4 (text(liters))/(100 text(km))`
Answer: D
6. Note that `1 le a le 4` because `5^5 >2012`, so we have four cases.
Start with a = 4. Then `b^2+c^2 = 2012 - 4^5` and `b = sqrt(2012-4^5-c^2)` . Enter `y = sqrt(2012-4^5-x^2)` into the Y= menu on the calculator and create a table starting at 1 with difference 1. Scroll down until the output becomes undefined and note that there are no integer possibilities for b with a = 4.
Now let a = 3 and create a table for `sqrt(2012-3^5-x^2`. Scroll down until you see c = 13 and b = 40 but note that b-c = 27 is not prime. Keep scrolling until you see c = 20 and b = 37; here b-c = 17 is prime. So a+b+c = 3+37+20 = 60.
Answer: E
7. It doesn't matter what the first digit is. Once we've selected the first digit, there are 4 (out of 5) choices for a different second digit, then 3 (out of 5) choices for a distinct third digit, etc. Thus the probability of having all the digits be different is:
`4/5 times 3/5 times 2/5 times 1/5 = 0.0384`
Answer: C
8. Let `r_B` be Bob's rate and `r_R` be Roy's rate. So `r_B cdot 1 + r_R cdot 1 = 60 => r_R = 60-r_B`.
We also know that:
`r_B(1 - 1/4 + 6/60) + r_R(1+6/60) = 60 => 17/20 r_B + 11/10 r_R = 60 => 17 r_B + 22r_r = 1200`
Substituting in `r_R = 60-r_B`:
`17r_B+22(60-r_B)=1200 => 120 = 5r_B => r_B = 24 =>r_R = 36 => r_R - r_B = 36-24 = 12`
Answer: B
9. `5/9 (F-32) = 5/9 (F+K) -K => 5(F-32) = 5(F+K)-9K => 5F - 160 = 5F -4K => -160 = -4K => K = 40`
Answer: D
10. Enter Y1 = 11*fpart(3X) into the Y= menu on the calculator. Create a table starting at 1 with difference 1:
1 2 3 4 5 6 7 8 9 10
3 6 9 1 4 7 10 2 5 8
So `a_8 = 5 => a_7 = 9 => a_6 = 3 => a5 = 1 => a_4 = 4 => a_3 = 5 => a_2 = 9 => a_1 = 3`.
Answer: B
11. Neither 1 nor 3 nor -3 are in the domain of f(x), hence cannot be in the domain of f(x)/g(x); g(-1) = 0, so -1 it is not in the domain of f(x)/g(x).
Answer: E
12. Let `log_2(x) = m` and `log_2(y) = n` where `m` and `n` are integers. Then `x = 2^m` and `y = 2^n` so `log_x(2) = log_{2^m}(2) = 1/m` and likewise `log_y(2) = 1/n`. Thus `1/m+1/n=1/2`.
If m = 1 or m = 2, there is no solution. If m = 3, then `1/3 + 1/n = 1/2 =>1/n = 1/6` so n = 6. Finally:
`xy = 2^m cdot 2^n = 2^6 cdot 2^3 = 2^9 = 512`
Answer: D
13. Graph `y = 3 sin(x)` and `y = 3 sin(3x)` on the interval `[0, 2pi)`; see below:
The graphs cross 6 times on this interval. Note that `2012/(2pi) approx 320.2197`, and `320 times 2pi = 640 pi` so the graphs cross `320 times 6 = 1920` times on the interval `[0,640pi)`. Now graph the functions on the interval `[640pi, 2012]` :
The graphs cross 2 more times, for a total of 1922.
Answer: C
14. P(4) = 77, so Q(4) = 7 and R(4) = 11 (or vice versa) and thus Q(4)+R(4) = 7+11 =18.
Answer: B
15. Position A at (0,0) and B at (60,0). The pitcher's rubber must be at `(43/sqrt(2),43/sqrt(2))`, so the distance between the rubber and B is:
`sqrt((43/sqrt(2)-60)^2 + (43/sqrt(2)-0)^2) approx 42.43`
Answer: A
16. Note that `(5n-8)/(2n+4)` must approach 2.5 as `n -> pm oo`. Enter `y = (5x-8)/(2x+4)` into the Y= menu on the calculator and create a table starting at 0 with difference 1. Note that 0, 4 and 16 all result in integer outputs, and after this the output values begin approaching 2.5. Now reset the table to start at 0 with difference 1 and scroll up through the negative numbers, noting that -4, -8 and -20 each result in integer outputs; after this, the output values begin approaching 2.5. This yields 6 possible values for n.
Answer: D
17. `a^2 = 2b^2-2 => a = sqrt(2b^2-2)` (because both a and b must be positive), so enter `y = sqrt(2x^2-2)` into the Y= menu on the calculator and create a table starting at 1 with difference 1. Scroll down until you see an integer in the second column: b = 3 and a = 4 don't work because 4+3 = 7 < 100; b = 17 and a = 24 don't work because 24+17 < 100; but a = 140 and b = 99 do work, so `a-b = 140-99 =41`.
Answer: E
18. Let `a_9 = x`. Then `a_{10} = a_8 + a_9 = 82+x` and `a_11 = a_{10}+a_9 = 82+x+x => 348 = 82+2x => x = 133`.
Answer: E
19. Draw a picture:
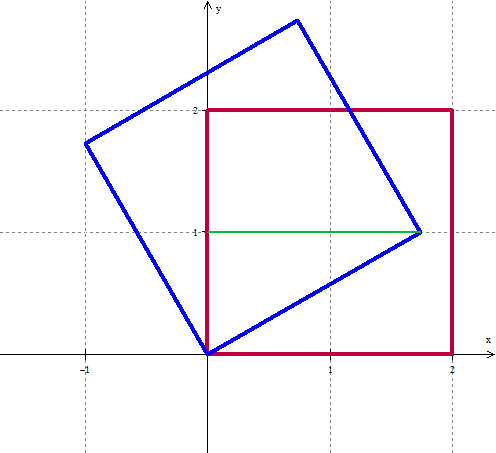
The intersection of the regions inside the two squares consists of a trapezoid and a triangle. The lower right corner of the original red triangle gets rotated to `(2cos(30^o),2sin(30^o)) = (sqrt(3),1)` so the area of the triangle is `1/2 (1)(sqrt(3)) = sqrt(3)/2`.
The slope of the blue line segment passing through (0,0) and `(sqrt(3),1)` is `1/sqrt(3)` so the slope of the blue line segment perpendicular to that is `-sqrt(3)`. The equation of the line passing through `(sqrt(3),1)` with slope `-sqrt(3)` is:
`(y-1)/(x-sqrt(3)) = -sqrt(3) => y-1 = -sqrt(3)(x-sqrt(3)) => y = -sqrt(3)x +4`
This line intersects the top of the red square (where y = 2) when `2 = -sqrt(3) x + 4 => sqrt(3)x = 2 => x = 2/sqrt(3)` . The area of the trapezoid is thus `(2/sqrt(3)+sqrt(3))/2 cdot 1 = (2/sqrt(3)+sqrt(3))/2 cdot sqrt(3)/sqrt(3) = (2 + 3)/(2sqrt(3)) = 5/(2sqrt(3)) = (5sqrt(3))/6 ` .
So the total area is: `sqrt(3)/2 + (5sqrt(3))/6 = (8sqrt(3))/6 = (4sqrt(3))/3` ` `
Answer: B
20. There are four cases: p = 1, p = 2, p = 3, p = 4.
When p = 1, q+r+s = 21, so there are 19 sub-cases: q = 1, q = 2, ..., q = 19. When q = 1, r can be any integer from 1 through 19; when q = 2, r can be any integer from 1 through 18; ...; when q = 19, then the only possibility is that r = 1 (so s = 1). So there are 19+18+...+3+2+1 or `(19 times 20)/2 = 190` subcases.
Similarly, when p = 2, q+r+s = 20, so q can be any integer from 1 through 18, and there are a total of 18+...+3+2+1 or `(18 times 19)/2 = 171` subcases.
For p = 3, there are `(17 times 18)/2 = 153` subcases; and for p = 4, there are `(16 times 17)/2 = 136` subcases. Thus the total number of cases is 190+171+153+136 = 650.
Answer: A